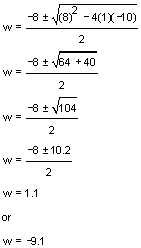Linear and Quadratic Functions: Determining a Quadratic Function

Real World Applications of Quadratic Functions (continued)

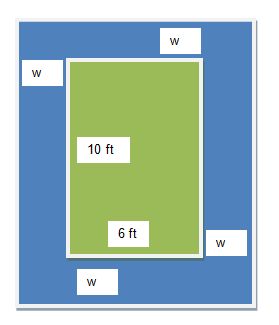
Let’s go through another problem. Suppose that you have a sandbox that is 6 feet by 10 feet. You want to build a deck around the sandbox that is equal in width on all sides. You want the total area of the sandbox and deck to equal 100 square feet. What is the width of the new deck that you want to build?

When faced with this kind of problem, the first step is to draw a diagram. This will help you visualize your problem.

Sandbox blueprint with dimensions six feet by ten feet and a deck with uniform width

We are able to write an equation for area that will help us solve for w (width of the deck).

Let A = l x w
100 = (2w + 10)(2w + 6)

Notice that in order to get the area of the sandbox and the deck around the sandbox you will have to add 2w to each dimension.

Multiply:

4w2 + 32w + 60 = 100
4w2 + 32w – 40 = 0

Divide the terms by 4 to simplify the quadratic equation.

w2 + 8w – 10 = 0

Use the Quadratic Formula to solve for w:

w equals negative 8 plus or minus the square root of 8 squared minus 4 times 1 times negative 10 all over 2. w equals negative 8 plus or minus the square root of 64 plus 40 all over 2. w equals negative 8 plus or minus the square root of 104 all over 2. w equals negative 8 plus or minus 10.2 all over 2. w equals 1.1 or w equals negative 9.1

You should throw out the negative value since we can’t have a negative width. Your answer therefore is approximately 1.1 feet.