Imaginary Numbers

No Real Solutions

You may be wondering how a quadratic function can have no real solutions. That happens when the graph of a function does not cross the x-axis. For example, the following quadratic function will not have any real solutions.

Graph of three x squared minus seven x plus five
Graph of 3x² – 7x + 5

Notice this graph does not cross the x-axis, therefore there will be no real solutions. On the other hand, there are imaginary solutions.

Imaginary Numbers

You may have been told in the past that you can’t take the square root of a negative number. That is not exactly true. You can take the square root of a negative number, but your solution will be imaginary. The following is the definition of imaginary numbers:

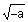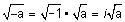If a > 0 then the imaginary number square root of negative a is defined as square root of negative a is equal to square root of negative 1 multiplied by square root of a is equal to i square root of a .
This means that 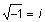square root of negative one equals i .

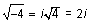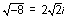For example, square root of negative four equals i times the square root of 4 equals two i and square root of negative eight equals two square root of two i .

Some of your solutions to quadratic functions may be imaginary. Let’s take a look at an equation with an imaginary solution. We know this equation has no real solutions because the discriminant (0² – 4(3)(48)) is a negative number (0 – 576 = -576). If we try to solve this equation by factoring we can see that there is no value of x that can make the equation equals zero.

3x² + 48 = 0

3(x² + 16) = 0

x² + 16 = 0

x² = -16 (There is no real number, that when squared, will equal a negative number)

For more information on imaginary and complex numbers, check out the website below:

The Purplemath website.

Once you have finished investigating imaginary and complex numbers, download this worksheet as a PDF, and keep it handy while you work in this unit. Download the key as a PDF and check your work.