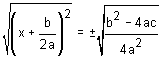Linear and Quadratic Functions: Solving Quadratic Functions

The Quadratic Formula

Students at desks

We can use the completing the square process to come up with a formula that is used to solve any quadratic function. This formula is called the Quadratic Formula.

Let’s go through how this formula is created.

Start with ax2 + bx + c = 0 and assume a ≠ 0.

Since we are completing the square, divide the entire equation by a.

x squared plus b over a times x plus c over a is equal to zero

Subtract the constant term from both sides of the equation.

x squared plus b over a times x is equal to negative c over a

Complete the square and simplify.

x squared plus b over a times x plus the quantity b over two a squared is equal to negative c over a plus the quantity b over two a squared

the quantity x plus b over two a squared is equal to negative four a c plus b squared over four a squared

Take the square root of both sides and simplify.

square root of the quantity x plus b over two a squared is equal to plus or minus square root of the quantity b squared minus four a c over four a squared

= x plus b over two a is equal to plus or minus square root of the quantity b squared minus four a c all over two a

Subtract b divided by 2 a  from each side of the equation and simplify.

x is equal to negative b over two a plus or minus square root of the quantity b squared minus 4 a c all over two a

x is equal to negative b plus or minus the square root of the quantity b squared minus four a c all over two a

Do you recognize the value inside the square root? It’s the discriminant. This makes sense since that value will tell you whether the answer will be imaginary or real. A zero value in the square root will also produce a double root.