Dilations on a Coordinate Axis
One way to imagine how dilation works is by shining a light on a figure. The image (shadow) the figure makes on the wall is a dilation of the original figure. The location of the light that is shining is the center of the dilation.
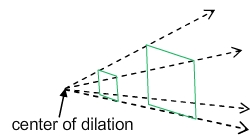 |
Dilation of a square |
On a coordinate axis, there is a center point for a specific dilation. In this course, we will use the origin as the center point.
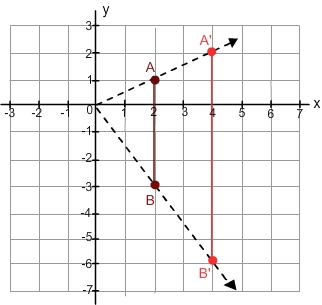
Take a look at the line segment AB, with end points A (2, 1) and B (2, -3). A dilation with center at the origin and a scale factor of 2 will produce a line segment A’B’. What are the coordinates of A’ and B’, the endpoints?
|
A’ = A·f |
B’ = B·f |
x-coordinate: |
x’ = 2·2 = 4 |
x’ = 2·2 = 4 |
y-coordinate: |
y’ = 1·2 = 2 |
y’ = -3·2 = -6 |
(x’, y’) |
A’ (4, 2) |
B’ (4, -6) |
Very simply, we multiplied each coordinate by the scale factor of 2 to get the new coordinate. Take a look at what the original line segment and the dilated line segment look like with respect to the origin.
 |
Dilation on a Coordinate Axis |
When the scale factor is negative or a fraction less than 1, it is not as easy to visualize the dilation with center at the origin. However, the calculations are just as simple. Each dimension of the new image is the corresponding dimension of the original image times the scale factor.
|
Summary: A’ = A·f, where f is the scale factor. |f| > 1, the dilation is an enlargement. |