Equations of a Circle Centered at the Point (h, k)
Circles with centers at a point other than the origin have a similar equation, but take into account the center point.
|
The standard equation for a circle centered at the point (h, k) with radius r is: (x – h)2 + (y – k)2 = r2 |
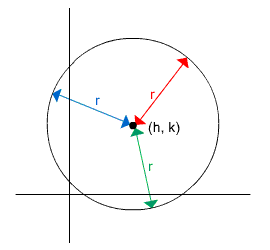
Circle centered at the point (h, k) with radius r
Example:
What is the equation of the circle centered at the point (3, 5) with radius 6?
Solution:
We are told that the center is (3, 5). This means h = 3 and k = 5. We are also told that r = 6.
Using the general equation (x – h)2 + (y – k)2 = r2, we get:
(x – 3)2 + (y – 5)2 = 62
(x – 3)2 + (y – 5)2 = 36
Example:
What is the center and radius of the circle defined by the equation (x – 6)2 + (y + 6)2 = 100?
Solution:
We need to be very careful with the signs of our numbers. Rearrange the equation so that it is in the general form (x – h)2 + (y – k)2 = r2.
(x – 6)2 + (y – (-6))2 = 102
Center: (6, -6)
Radius: r = 10
