Radioactive Decay

So what does exponential decay have to do with dating rocks? Well, many atoms spontaneously change into other kinds of atoms through a process called radioactive decay. There are several types of radioactive decay, but all take place when an unstable nucleus spontaneously breaks down or loses protons. If the number of protons in the atom’s nucleus changes, the atom becomes a different element with new physical and chemical properties. For example, if potassium lost one proton from its nucleus, it would no longer be potassium; it would be argon because it would now have 18 protons in its nucleus instead of 19 protons. Any substance with unstable nuclei is called radioactive because it will decay in this way.

Parent and Daughter

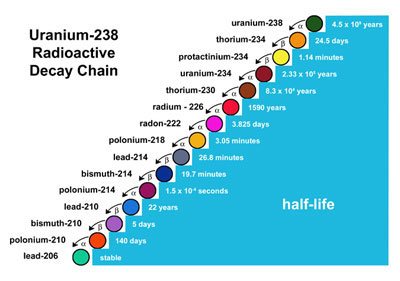
The decay chain from Uranium-238 to Lead-206

The atom that decays is the parent isotope and the resulting product is the daughter isotope. Here you see how an atom of Uranium-238 (the parent isotope) decays to an atom of Lead-206 (the daughter isotope). Radioactive isotopes do not decay at the same rate; each decays at its own distinctive rate, which has been carefully measured. Decay rates are NOT affected by environmental conditions, like temperature, but are constant for each given isotope. The rate of decay is called half-life, which is the amount of time it takes for one-half of a parent isotope to decay to the daughter isotope. In other words, half the original atoms of the parent isotope decay in one half-life. Half-life values range from a few seconds for some types of isotopes to billions of years for others, as the table shows.

Parent Isotope	Daughter Isotope	Half-life (years)
Uranium-235	Lead-206	4.5 billion
Potassium-40	Argon-40	1.25 billion
Carbon-14	Nitrogen-14	5,730
Hydrogen-3	Helium-3	12.3

Based on the information in the table, can you answer the following questions?

If you start with 100 grams of carbon-14 atoms, how many grams will you have in 5,730 years?

After one half-life, or 5,730 years, one-half of the parent isotope will decay to the daughter isotope. After 5,730 years, you will have 50 grams of carbon-14.

If you start with 100 grams of hydrogen-3, how many grams will you have after 24.6 years?

After 24.6 years, two half-lives will have passed. You will have 25 grams left.

Half-Lives

Number of Half-lives elapsed	Fraction Remaining
0	1/1
1	1/2
2	1/4
3	1/8
4	1/16
5	1/32
6	?

What fraction of the substance would be left after 6 half-lives?

Since the denominator doubles with each half-life, the fraction of material left after 6 half-lives would be 1/64 of the original amount. Here is a challenge for you: Can you come up with a formula for the remaining fraction of material when "n" is the number of half-lives?

The concept of radioactive decay is crucial to absolute dating because it acts like a clock that records how much time has elapsed since a mineral crystallized. The proportion of daughter atoms to parent atoms in a rock reveals the number of half-lives that have elapsed since the rock crystallized. Multiply the length of the half-life by the number of elapsed half-lives to obtain the rock’s age. For example, suppose you find a fossil in a rock and you find that the proportion of parent isotopes to daughter isotopes is 1:4. This means that 75% of the parent atoms have decayed to daughter products and that two half-lives have elapsed. If the parent isotope’s half-life is one billion years, then multiply one billion years by two and you find that this rock is two billion years old. With tables of known half-lives like you saw earlier, scientists can assign an absolute age to many Earth materials after they sample them to find the ratio of parent to daughter isotopes.