Electric Potential Energy

You can define electric potential energy just like you define gravitational potential energy—it is depending on the charge’s position in an electric field. Take for example a positive test charge (always assume the test charge is positive unless otherwise stated). It takes a certain amount of energy to move the test charge in the field. The work-energy theorem still holds true, so you can assume that the magnitude of the change in the potential energy is going to be equal to the work done on it.

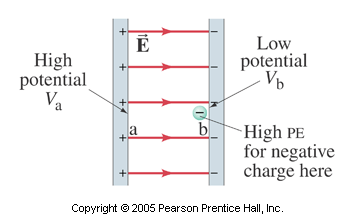
Notice in the diagram above, the positive test charge would be repelled by the positive plate and attracted to the negative side. In this case, the test charge would have a high potential at point a and a low potential at point b. Think of it this way—the charge “wants” to be near the negative side just like a ball "wants" to be near the ground. To move the test charge away from this position takes work. The work done in an electric field, E, to move the change a distance, d is:

And, since in this case, the electric field is constant, the charged particle also undergoes a constant electrostatic force. It will undergo constant acceleration and thus gain kinetic energy that is equal to its change in potential (just like the falling ball example, except turned sideways).

Suppose you have a negative test charge (an electron) instead and it is placed near the negative plate. If the electron is free to move, will its electric potential energy increase or decrease? An electron released at point b will move toward the positive plate. As the electron moves toward the positive plate, its potential energy decreases as its kinetic energy gets larger.