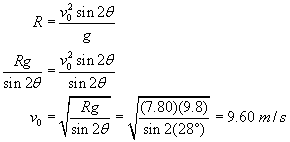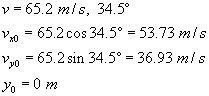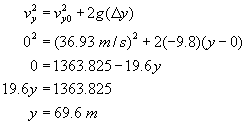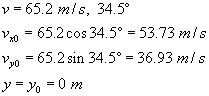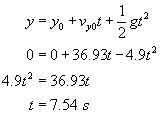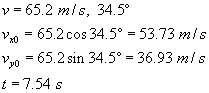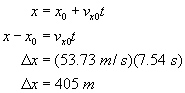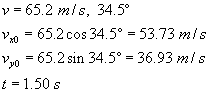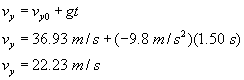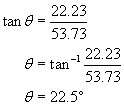Projectile Motion Self-Check
Projectile Motion Self-Check
Now, you try. Complete the self-check activity by working out the problems, and then clicking on the question to review the explanation.
A projectile is fired with an initial speed of 65.2 m/s at an angle of 34.5° above the horizontal on a long flat firing range. Determine:
 More Practice Problems
More Practice Problems
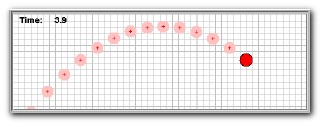
Problem 1
Click the image below to view Problem 1.

Next »
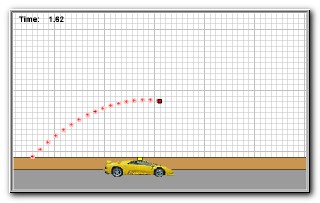
Problem 4
Click the image below to view Problem 4.
« Previous
 For more practice, solve the following problems from "Chapter 3, Problems" at the end of the chapter. The answers are in the back of your book.
For more practice, solve the following problems from "Chapter 3, Problems" at the end of the chapter. The answers are in the back of your book.
Problems # 19, 23, 27, 31, 35
© 2009 KC Distance Learning. All rights reserved.
 Projectile Motion Self-Check
Projectile Motion Self-Check More Practice Problems
More Practice Problems For more practice, solve the following problems from "Chapter 3, Problems" at the end of the chapter. The answers are in the back of your book.
For more practice, solve the following problems from "Chapter 3, Problems" at the end of the chapter. The answers are in the back of your book.