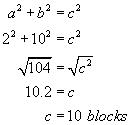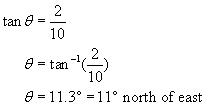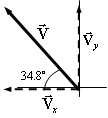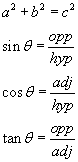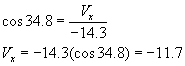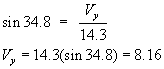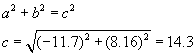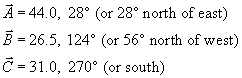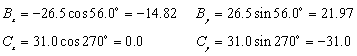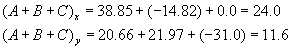Kinematics: Two-Dimensional Motion

self check Self Check: Vector Resolution

Now, you try. Complete the self-check activity by working out the problems, and then clicking on the question to review the explanation.

think and click icon
A delivery truck travels 18 blocks north, 10 blocks east, and 16 blocks south. What is its final displacement from the origin? Assume the blocks are of equal length.
Given:
18 blocks, N

10 blocks, E

16 blocks, S		 Diagram:
diagram of vector resolution from problem
Find:
Resultant distance, Vector D sub R		 Equations:
a squared plus b squared equals c squared; tangent theta equals opposite over adjacent
Solution:
The truck has a displacement of 18 + (-16) = 2 blocks north and 10 blocks east.

Find the resultant magnitude:

a squared plus b squared equals c squared; two squared plus ten squared equals c squared; square root of one hundred four equals square root of c squared; ten point two equals c; c equals ten blocks

Find the direction of the resultant:

tangent theta equals two over ten; theta equals inverse tangent of the fraction two over ten; theta equals eleven point three degrees equals eleven degrees north of east;

think and click icon
Vector Vector V is a vector 14.3 units in magnitude and points at an angle of 34.8° above the negative x-axis. (a) Sketch this vector. (b) Find Vx and Vy. (c) Use Vx and Vy to obtain (again) the magnitude and direction of Vector V. [Note: Part (c) is a good way to check if you’ve resolved your vector correctly.]
Given:
Vector V equals fourteen point three units, thirty four point eight degrees north of west		 Diagram:
diagram of vector V from problem
Find:
Vx, Vy, and Vector V		 Equations:
a squared plus b squared equals c squared; sine theta equals opposite over hypotenuse; cosine theta equals adjacent over hypotenuse; tangent theta equals opposite over adjacent
Solution:
Find the components:

cosine of thirty four point eight degrees equals v sub x over negative fourteen point three; V sub x equals negative fourteen point three times cosine of thirty four point eight degrees equals negative eleven point seven

sine of thirty four point eight degrees equals V sub y over fourteen point three; V sub y equals fourteen point three times sine of thirty four point eight degrees equals eight point one six

Find the magnitude of the resultant of Vx, Vy, and Vector V

a squared plus b squared equals c squared; c equals the square root of the quantity of the square of negative eleven point seven plus the square of eight point one six end quantity equals fourteen point three

Find the direction of the resultant:

tangent theta equals eight point one six over negative eleven point seven; theta equals inverse tangent of the fraction eight point one six over eleven point seven; theta equals thirty four point eight degrees north of west

Notice we changed 11.7 to a positive number. We wanted the reference angle and would deal with the actual direction using north of west.

diagram of the 3 vectors from the problem

think and click icon
Three vectors are shown in the diagram above. Their magnitudes are given in arbitrary units. Determine the sum of the three vectors. Give the resultant in terms of (a) components, (b) magnitude and angle with the x-axis.
Given:
Three vectors:

Vector A equals forty four point zero, twenty eight degrees or twenty eight degrees north of east; Vector B equals twenty six point five, one hundred twenty four degrees or fifty six north of west; Vector C equals thirty one point zero, two hundred seventy degrees or south
Find:
Ax , A y, B x, B y, C x, C y, R x, R y , vector R		 Equations:
a squared plus b squared equals c squared; sine theta equals opposite over hypotenuse; cosine theta equals adjacent over hypotenuse; tangent theta equals opposite over adjacent
Solution:
First, find the components of each vector:

A x equals forty four cosine twenty eight point zero degrees equals thirty eight point eight five; A y equals forty four sine twenty eight point zero degrees equals twenty point six six
B x equals negative twenty six point five cosine fifty six point zero degrees equals negative fourteen point eight two; B y equals twenty six point five sine fifty six point zero degrees equals twenty one point nine seven; C x equals thirty one point zero times cosine two hundred seventy degrees equals zero point zero; C y equals thirty one point zero times sine two hundred seventy degrees equals negative thirty one point zero

(a) Then, find the resultant components:

The quantity A plus B plus C end quantity sub x equals thirty eight point eight five plus negative fourteen point eight two plus zero point zero equals twenty four point zero; The quantity A plus B plus C end quantity sub y equals twenty point six six plus twenty one point nine seven plus negative thirty one point zero equals eleven point six

(b) Then, find the magnitude of the resultant:

c equals the square root of the quantity twenty four point zero squared plus eleven point six squared end quantity, equals twenty six point seven.

And the direction of the resultant:

tangent theta equals eleven point six three divided by twenty four point zero; Theta equals inverse tangent of the fraction eleven point six three over twenty four point zero; Theta equals twenty five point eight degrees north of east

 

self check More Vector Self-Check

In this activity, you will review addition of displacement vectors. Use this worksheet to help organize your notes. Click the image below to view the animation.

View the animation.