Module 6: Lesson 6-1a: Antiderivatives and Slope Fields

Introduction

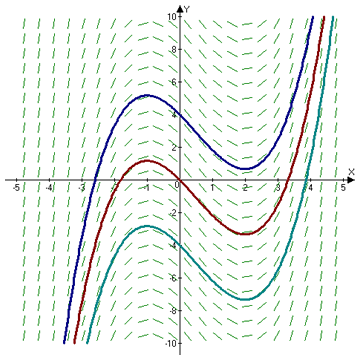In this section we go over the process of finding antiderivatives so that we can solve indefinite integrals in both the general case and when we are given initial conditions that allow us to find the value of the constant of integration.  We will also look at slope fields, something you will be sure to see on the AP exam.  Slope Fields allow us to look at a field of short segments that represent the slopes of the tangent lines along a curve and thus guess at the shape of the curve. Look at the image to the right. It is an example of the slope field of dy/dx=x²-x-1, with the blue, red, and turquoise lines being (x³/3)-(x²/2)-x+4, (x³/3)-(x²/2)-x, and (x³/3)-(x²/2)-x-4, respectively.

Objective: We address topic 2 (pdf) in the AP course outline. By the end of this section you will be able to give a geometric interpretation of differential equations using slope fields and know the relationships between slope fields and solution curves for differential equations.  You will also be able to solve an initial value problem, finding the value of the constant of integration using the information you are given.

Topics in this section include:

1. 6-1.1 Solving Initial Value Problems
2. 6-1.2 Slope Fields - What They Are
3. 6-1.3 Slope Fields - How to Construct Them
4. 6-1.4 Antiderivatives and Indefinite Integrals
5. Using the FTC to Solve an Initial Value Problem

Guiding Questions

As you navigate through this section, ask yourself the following questions:

1. If I give you a curve, how do you think you could construct a visual representation of that curve using nothing but short line segments?
2. What is the relationship between finding a derivative and finding an antiderivative?

Now that you are familiar with the topics we will cover in this section of Module 6, you are ready to begin. Please click the menu item under Section called Solving Initial Value Problems to begin 6-1.1 Solving Initial Value Problems.

Photo Attribution
Description: The slope field of dy/dx=x2-x-1, with the blue, red, and turquoise lines being (x3/3)-(x2/2)-x+4, (x3/3)-(x2/2)-x, and (x3/3)-(x2/2)-x-4, respectively.
Source: Wikimedia Commons